Why does isotropy matter?
Neural Cellular Automata (NCA) can build and persist complex patterns on a grid starting from a single seed cell. Patterns are constructed by repeatedly updating cells using the same learned rule. Cells can only see the states of the cells in their tiny neighbourhood, and updates happen asynchronously without relying on the global clock. The system appears to be fully self-organising and capable of solving the pattern-construction task without relying on any external guidance. However, the original Growing NCA
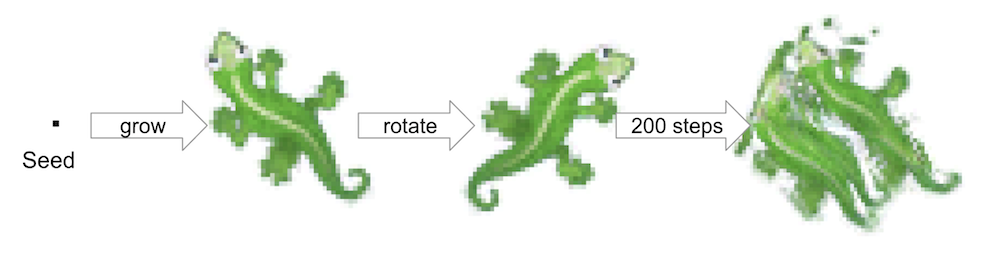
In the growing NCA paradigm, each cell's state is represented by a number of scalar values, or "channels." The first three channels represent RGB colours, while the fourth "alpha" channel determines whether the cell is dead or alive. Let's consider the following experiment: take the NCA model capable of growing a lizard pattern and rotate the grid state about an imaginary "z-axis" in the centre, after the pattern has developed and stabilised. We can do this by resampling each of the state channels (RGBA+latent) as if they were grayscale images. Of course, the resampling procedure may introduce some error, but even for perfect 90-degree rotation the previously stable pattern undergoes a dramatic transformation.
Naturally, one would expect the pattern to remain stable after this rotation, just as real-world creatures don't usually disintegrate while turning around. However, this is not the case with the original NCA implementation. Why does this happen? Many classic cellular automata (CA) do not encounter this problem. For instance, complex structures built in the Game of Life continue to function even after a 90° rotation or reflection. In the cellular automata literature this type of CAs is often called isotropic.
A more precise name would be equivariant, which means that if we apply some transformation to the system state, the subsequent behaviour of the system would match the untransformed version up to the same transformation. In this article we are going to discuss systems that are equivariant to rotations and reflections (in addition to translation which is true for all CAs). To match the previous conventions we'll call rotation equivariant models steerable, and rotation-reflection equivariant – isotropic.
Invariance is the concept closely related to equivariance which means being independent or insensitive to a particular class of transformations. In general we are going to design equivariant CAs by requiring invariance of their local rules to a particular class of transformations.
To be fair, most biological systems are not fully isotropic or even rotation equivariant as they have an inherent chirality, and the environment they grow and live in generally has some directional cues. For example, gravity produces a very prominent axis that influences the development of many organisms, especially plants. Earth's magnetic field and average wind or light directions are also perceived by many creatures. Finally, maternal gradients of chemicals are reliably observed in pattern formation and embryogenesis. Nevertheless, many developmental processes can be seen as isotropic to a large extent, which is confirmed, for example, by microgravity vertebrate reproduction experiments
Isotropy and chirality are such fundamental properties of nature that we would like to train NCAs with these properties. This would necessitate modifying the NCA architecture and training method. In a series of recent publications, we explored different types of isotropic architectures and how to train them. The goal of this article is to provide an overview of these methods.
We will do this step by step, starting with an analysis of the original NCA architecture and the source of its anisotropy. Then we relax the architecture by giving cells control of their own orientation. Finally, we make the model entirely isotropic by stripping any directional perception from cells. Throughout our experiments, we will also describe which training issues arise and how we solved them.
Anisotropy in Neural Cellular Automata
Let's look at the original Growing NCA
Let's have a closer look at the NCA update rule to see where the anisotropy comes from and how to fix it.
The first step of the update rule is perception, in which scalar fields representing cell state channels are convolved with a fixed set of filters. Examining the filters immediately reveals the source of anisotropy: Sobel kernels. They measure the differences between the state values of neighbours on the different sides of a current cell. As a result, for example, rotating the grid 180° would reverse the signs of the Sobel filter outputs.
These Sobel kernels estimate partial derivatives of the cell state fields along the x- and y-axis separately. We can imagine them as two perpendicular sensors that all cells are equipped with. These sensors are directionally aligned for all cells, which can be seen as a strong externally-given coordination factor.
This coordination is sometimes realistic and makes training much easier. In fact, it enables NCA to grow a specific pattern in a specific orientation starting from the symmetric single-cell configuration. That's why we could train the model using the simple pixel-wise L2 loss against a target image. Unfortunately this simplicity makes it impossible for multiple differently oriented patterns to exist in the same world, which seems like a serious limitation of the model.
The first modification we propose to the original architecture will be a relaxation that will preserve chirality, widespread in nature and in human-made systems, but will remove the extrinsic global alignment required by the original architecture.
Steerable NCA
The core idea of Steerable NCA (
Angle-based steering
One approach is to use one of the internal states of each cell to represent its individual rotation angle. Cells can incrementally modify their own orientation by steering clock- or counterclockwise, but not directly perceive it. However, their entire perception - the way they each face - would be rotated according to this angle. We assume that all cells are initialised with a random orientation at the beginning of the simulation.
The cell's perception vector $\mathbf{p}$ is computed as follows, with input $(\mathbf{s}, s_\theta)$, where $\mathbf{s}$ is a 2D array of vectors representing cell states, and $s_\theta$ are their rotation angles.
$$ \begin{aligned} \begin{bmatrix} \mathbf{p}_x \\ \mathbf{p}_y \end{bmatrix} &= \begin{bmatrix} \cos(s_\theta) & \sin(s_\theta) \\ -\sin(s_\theta) & \cos(s_\theta) \end{bmatrix} \begin{bmatrix} K_{\text{sobx}} \ast \mathbf{s} \\ K_{\text{soby}} \ast \mathbf{s} \end{bmatrix}\\ \mathbf{p} &= \text{concat}(\mathbf{s}, K_{\text{lap}} \ast \mathbf{s}, \mathbf{p}_x, \mathbf{p}_y) \end{aligned} $$Where $K_{\text{sobx}}, K_{\text{soby}}$ are the Sobel filters, and $K_{\text{lap}}$ is a symmetric Laplacian filter, which we will talk about later in this article while discussing the fully isotropic NCA. Now we can rotate the pattern and it will persist as long as we adjust $s_\theta$ accordingly. Rotation angles different from 90° introduce resampling errors on square grids (and non-60° on hexagonal grids), but we'll see later that our models are quite tolerant of them.
Gradient-based steering
Another variant of the self-steering model is inspired by the alignment of the real world cells to chemical gradients, which is often observed in living systems. These gradients can be both externally provided and internally produced by the cell colony itself. Thus, cell orientation becomes an emergent property of the collective cells. It should not exist if a cell is alone, or if cell states are uniform. Only when cells differ from one another, should they care about orientation, and it will be a property of their neighbourhood, and not the cell itself.
In this variant, we assign a special meaning to one of the cell state scalar fields $s_\text{align}$. Cells are going to align their sensors along the gradient of this field. The local coordinate frame is built on the L2-clipped gradient of $s_\text{align}$, estimated with a pair of Sobel filters. Gradients of other fields are transformed into this local frame before being perceived by the cell. In the case where the cell orientation is poorly defined due to locally uniform $s_\text{align}$, perceived state gradients are effectively multiplied by zero.
The cell's perception vector $\mathbf{p}$ is computed as follows, with input $\mathbf{x} = (\mathbf{s}, s_\text{align})$:
$$ \begin{aligned} \mathbf{g}_{\text{align}} &= [K_{\text{sobx}} \ast s_{\text{align}} , K_{\text{soby}} \ast s_{\text{align}}] \\ [u_\theta, v_\theta] &= \mathbf{g}_{\text{align}} \big/ \max(\|\mathbf{g}_{\text{align}}\|, 1) \\ \begin{bmatrix} \mathbf{p}_x \\ \mathbf{p}_y \end{bmatrix} &= \begin{bmatrix} u_\theta & v_\theta \\ -v_\theta & u_\theta \end{bmatrix} \begin{bmatrix} K_{\text{sobx}} \ast \mathbf{s} \\ K_{\text{soby}} \ast \mathbf{s} \end{bmatrix}\\ \mathbf{p} &= \text{concat}(\mathbf{x}, K_{\text{lap}} \ast \mathbf{x}, \mathbf{p}_x, \mathbf{p}_y) \end{aligned} $$Note how in this variant, cells can also perceive values $s_\text{align}$ without breaking the rotation invariance. Now, to rotate a state, it's sufficient to resample state values without any additional adjustments to the state components.
How models break symmetries
Unless the target pattern is perfectly radially symmetrical, its construction from the perfectly symmetrical seed cell will break some degrees of symmetry, such as left-right symmetry. This implies that cells in equivalent positions on the left and right sides of some axis must behave differently.
One simple way of breaking the symmetry is to provide asymmetrical starting conditions. In the case of an explicit angle-based model, the symmetry is already broken by the orientation of the seed cell. As a more general solution we use spatial arrangements of multiple seed cells as a starting state.
However, the case of perfectly symmetrical initial conditions is particularly interesting, because models capable of building the asymmetrical pattern in this situation would demonstrate capabilities to achieve distributed consensus on the resulting pattern orientation. Some source of randomness is required to break the symmetry between cells at the "microscopic" level, so that the system can amplify those asymmetries to the "macroscopic" level.
The original NCA model uses stochastic cell updates to remove the assumption of a global clock controlling all cells. In this work the stochastic update mechanism plays the key role of the source of randomness that learned rules exploit for "microscopic" symmetry breaking.
Interestingly, we observed that some models trained in a stochastic regime managed to find an alternative source of randomness when deployed in a fully deterministic synchronous environment! They found a way to amplify floating point rounding errors of an otherwise symmetric Laplacian convolution.
How to train steerable NCA
Whichever model variant we choose, we still haven't answered the big question: how do we train such architectures?
Remember anisotropic NCA: we used a pixel-wise L2 loss between the generated pattern and a target image. This loss is not invariant to translation, rotation, or reflections. That is, the loss decreases only for patterns centred always in the same position, rotated by 0 degrees (patterns that are in the upright position), and with the proper reflection of the image. This is easily achievable with anisotropic NCA, since placing a seed in the centre fixes the translation ambiguity, while rotation and reflections are uniquely determined by their fixed anisotropic Sobel filters.
So how would steerable NCA fare with the same loss and the same initial conditions? Well, translation is not an issue, since we could still place a seed at the centre of the image during training. However, cells might decide to self-organise and form a pattern that is structurally correct but rotated by some random angle with respect to the target image. This is because there is one extra unspecified degree of freedom that needs to be resolved, encoded by the model's variable orientation. This precludes our traditional pixel-wise L2 loss since it would attempt to match our model's randomly-rotated image with the fixed upright target. Reflection would still not be an issue because all cells have the same intrinsic chirality determined by the handedness of the local coordinate frames produced by the x- and y-field "sensors" of each cell.
We will present two solutions for the rotation-invariance problem: first, by using initial conditions to force our steerable NCAs to always generate an upright image during training, and second, by enhancing the loss function itself to be rotation invariant.
Removing ambiguity using initial conditions
Let us, for now, proceed with the same pixel-wise L2 loss function applied with the same fixed upright target pattern used to train anisotropic NCA. One way we can prescribe desirable growth behaviour is by introducing some strategic bias via multiple seeds. In fact, with some care in how these seeds are configured, we'll see that we can remove the degree of freedom of rotation entirely. This is not an entirely new idea, and is in truth one that is deeply rooted in nature, resembling the use of maternal gradients and gravity to remove ambiguity in pattern formation and embryogenesis.
In the case of steerable NCA, we can easily define more restrictive initial conditions which break the up-down symmetry by initialising the system with two different seeds (different in that the two seeds are initialised with different state values) placed slightly apart from one another. Here, each seed serves as a point of origin for one of two sub-regions of the resultant shape. We need only choose an arbitrary "training configuration" for the two seeds. From there, we can use the same pixel-wise L2 loss used to train anisotropic NCA, and with no further augmentation. But how does having two seeds instead of one make any difference?
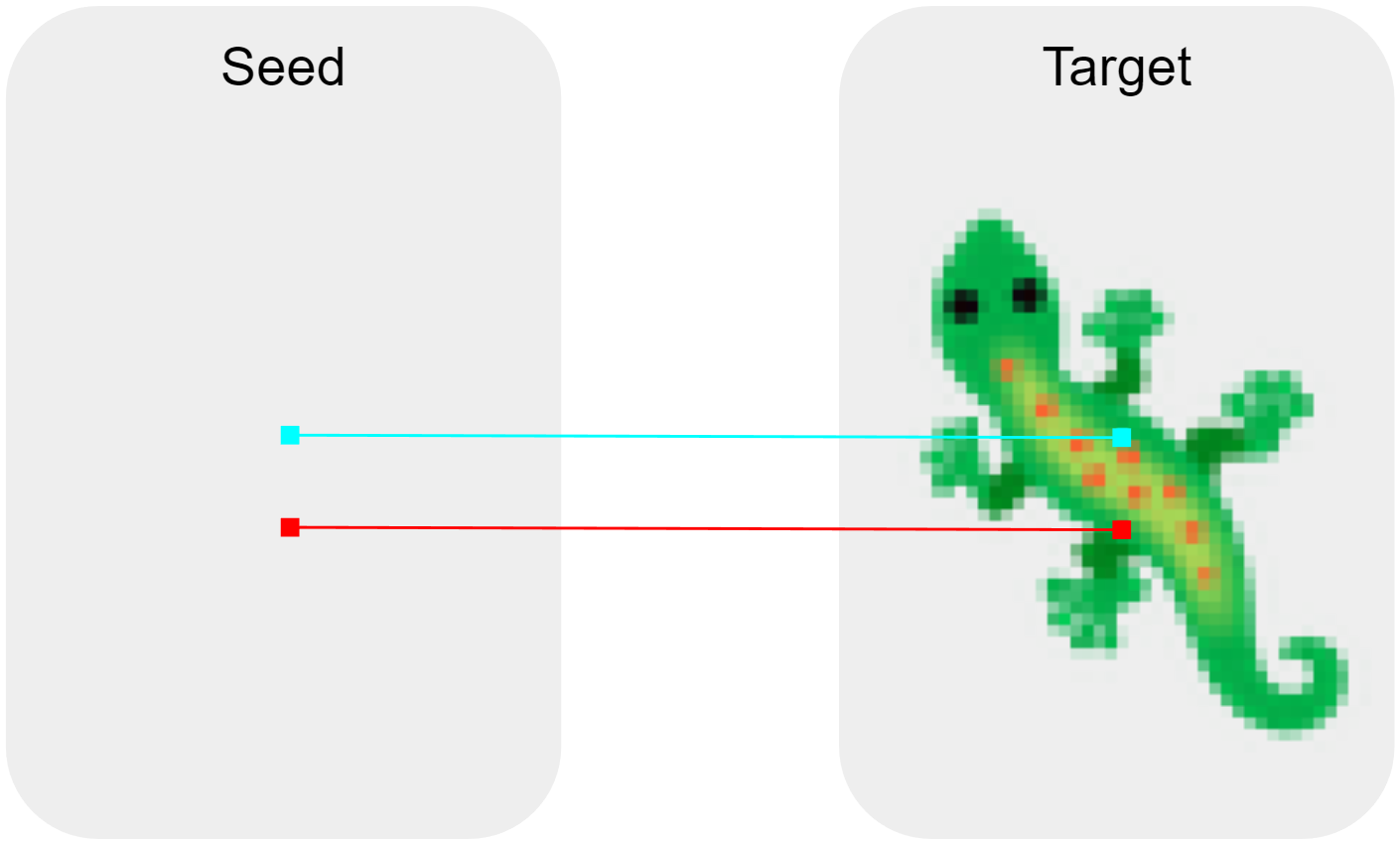
As an example, consider two seeds used to grow the lizard pattern. Distinguishing them by colour and fixing their arrangement during training gives steerable NCA a clear axis it can exploit in order to construct the target pattern. Since this is the only directional cue it has, the model does what we'd expect and learns to use the seeds as a framework for self-orientation. Each seed here roughly corresponds to half of the lizard, and as these halves grow, their intersection is the catalyst that provides the axial cue. If we then re-orient the seeds out of training, we find that the model constructs the pattern facing this new direction.
We can generalise this idea of configured initial conditions under the aptly-named paradigm of Structured Seeds. Later, we'll see isotropic NCA proceed with the same idea of mind, but require a more comprehensive seed structure to facilitate orientation.
Results
With our two-seed initial conditions, we now have something to play with: by adjusting the rotation of the seed structure out of training, we can take advantage of each region's dependence on the other's position to self-orient and actually dictate the direction in which steerable NCA will grow!
What if instead of rotating the seed structure, we adjust its other major property, the diameter? While the model can recover from minor distance perturbations and produce a stable pattern, placing the seeds too close or too far away from one another invariably changes the states of the cells at the point of intersection. We see some recurring patterns emerge in this often unpredictable environment: placed too close to one another, the seeds are unable to provide a clear axis of alignment; placed too far apart, they begin producing patterns before they've had a chance to orient with one another.
To get a better idea of what's going on, let's visualise the perception angle of each cell, and take a look at snapshots before, during, and after the model determines its orientation. Here, the cells are initialised at random angles, and over time (approximately 30 steps), the two growing regions originating from each seed cell intersect. At this point, we see the model start to "decide" its orientation, represented by an emerging coherent vector field.

By adjusting the rotation of the seed structure, all we're really doing is adjusting the point of intersection between the two regions. For example, if this point occurs to the right of the blue seed and the left of the red seed, the intersection will propagate throughout the two regions, orienting the upper and lower halves of the lizard counterclockwise, thus rotating the entire lizard by 90 degrees. It's worth noting that we don't see the cells all orient in the same direction; rather, the vector field stabilises to resemble a flow field based on the model's orientation.
Rotation invariant training
The solution above produces a growth dynamics that is fully determined by the initial seed configuration. It would be interesting to have models whose growth behaviour is less reliant on the initial conditions, and where the resulting pattern orientation is the result of collective decision-making among the self-organizing system of cells.
We know that our asynchronous updates generate noise capable of breaking symmetries, but this is not enough. The problem is the pixel-wise L2 loss on the target image, which is not rotation invariant. Hence, we introduced a rotation invariant loss that matches a given NCA pattern with any possible rotation of a target image, and selects a loss representing the minimum across all rotations. We need the loss to be only rotation invariant, since the position of the seed takes care of translation ambiguity and Sobel filters take care of reflection ambiguities.
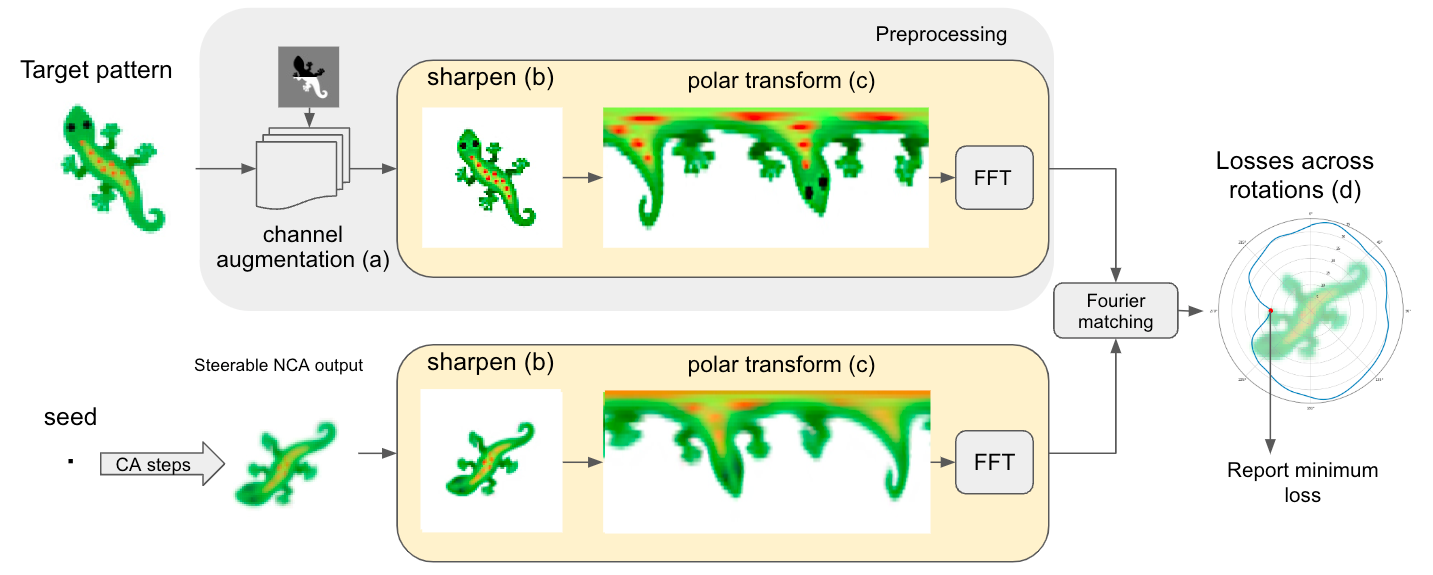
The rotation-invariant loss occasionally generates some undesirable local minima in the loss landscape, for instance when target images are similar to rotated versions of themselves. We observed that it is essential to augment the target image with extra channels that encourage symmetry breaking, which changes the loss landscape and makes the training regime more likely to converge to the desired configuration. In our paper, we also explain how to efficiently implement this by using fast Fourier transform (FFT). We refer to the paper if the reader is interested in more details.
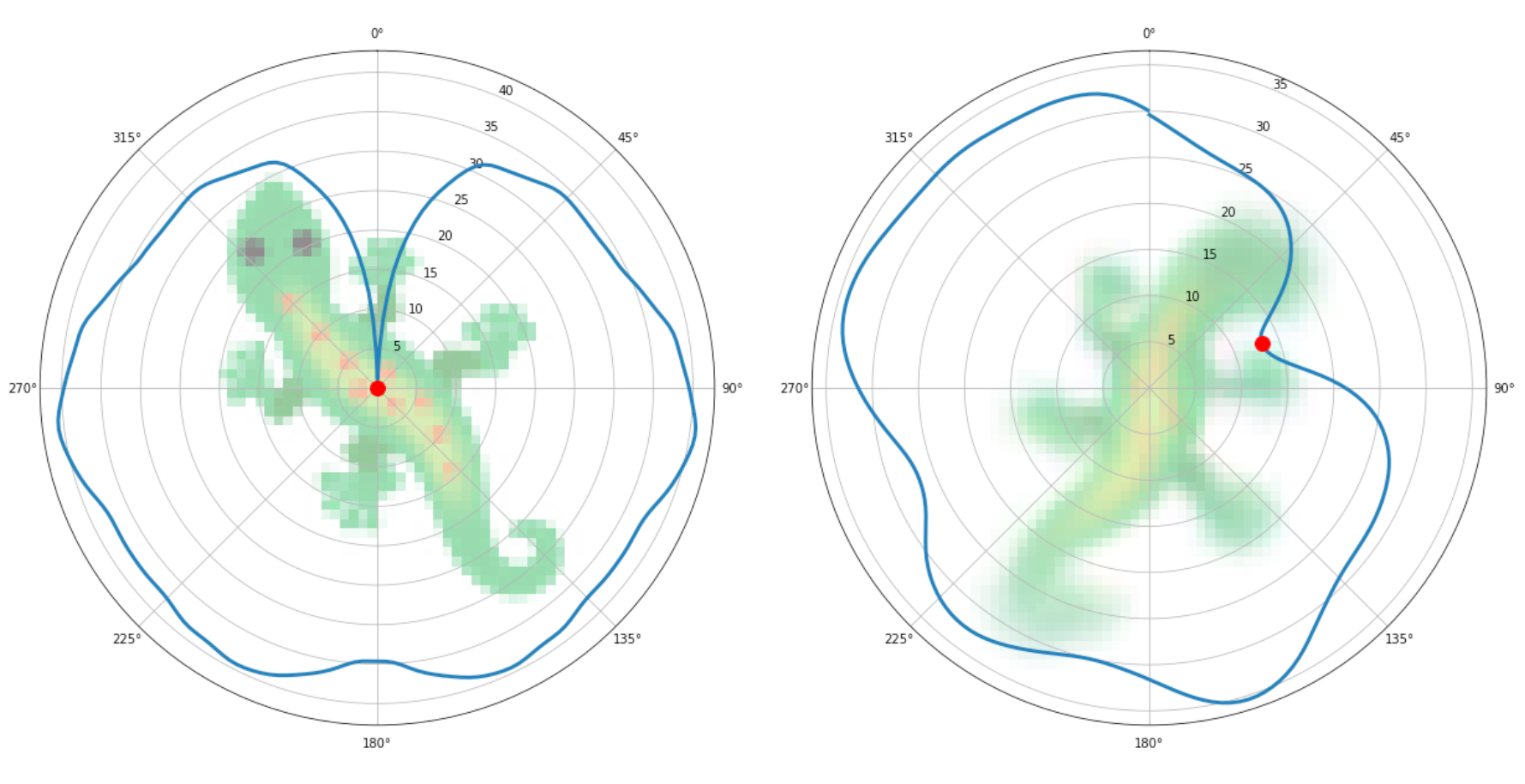
Below, you can see how the rotation-invariant loss is computed: to the left, as a reference, we calculate the loss with respect to the target pattern for every rotation and the minimum value is at the angle 0, where the pattern is upright. To the right, we calculate the loss of a pattern that is not fully formed and during training. The minimum loss is found at roughly 60 degrees, and it gets "selected" for the backpropagation step.
Results
With this rotation invariant training, the resulting patterns arise with a new random orientation every run, as expected.
As a side-effect of the training loss, which is rotation invariant, most patterns tend to slowly rotate over several steps: all rotations of the pattern have effectively the same loss, thus a rotating solution found by the model is just as valid as any static solution under our loss function. This quirk seems to decrease the longer we train the patterns, and having auxiliary losses can get rid of any unwanted movements of patterns.
We can also inspect the angles of the cells and see interesting differences between the angle- and gradient-based variants. Below are the angles generated by these variants for the lizard pattern:

On the left, the angle-based variant seems to generate some angle spirals at the centre of the pattern, going outwards. Also, the tail seems to have angles rotating following the direction of the tail. On the right, the gradient-based variant is incapable of creating spirals by construction, as there cannot be a discontinuity in the angles of nearby cells. Instead, we observe manifolds where angles are suppressed, likely generating a smoother transition among different directions.
Isotropic NCA
In the previous section we discussed modifications of the NCA model that remove global alignment between cells, while retaining the Sobel filters. In the Isotropic NCA (
The simplest filter that comes to mind is the Laplacian filter. A square-grid version of this filter can be represented by this convolutional kernel:
$$ K_{lap} = \begin{bmatrix} 1 & 2 & 1\\2 & -12 & 2 \\1 & 2 & 1 \end{bmatrix} $$In general, this filter estimates the difference between the state of the cell and the averaged state of its neighbours. In the Self-Organizing Textures
In the Growing Isotropic NCA paper, we use this filter only. After its publication, we experimented with another kind of isotropic filter that enhances the perception by adding additional perception of the magnitudes of spatial gradients in the neighbourhood. This filter makes use of Sobel filters, but instead of exposing them directly for the model to use, it aggregates them into magnitude values, maintaining the isotropic property of the system. We observed that this addition makes training faster, and our code base has the option to add this gradient norm filter to the isotropic experiments.
Just like with steerable NCA, isotropic NCA requires some way to break symmetries. Here as well, we use asynchronous cell updates to grant them this capability. Likewise, having different initial conditions for different seeds can also enable symmetry breaking.
Training isotropic NCA is even harder than steerable NCA, since now the system has to reliably break two symmetries in order to form a 2D pattern. We will demonstrate the two approaches we used to solve this problem: the first is by using a rotation-reflection invariant training and relying solely on asynchronous cell updates to break symmetries, while the second is by setting up initial conditions by means of structured seeds: placing multiple different seeds as the initial state of the system.
Rotation-reflection invariant training
Since isotropic NCA need to break two symmetries, this introduces the interesting problem that, in theory, they could generate a pattern with arbitrary rotations and reflections. Put another way, it is impossible to train an isotropic NCA starting from a single seed to match a pattern unless we try to match it to all rotations and reflections of such a pattern. As usual, translation ambiguity is still resolved by placing a seed always at the centre of the target image during training.
Therefore, we have to enhance the rotation-invariant training that we used for Steerable NCA and transform it into a rotation-reflection invariant training. This is very simple to do: we match our candidate NCA with all rotations for both the target image and a reflected version of the target. Then, we choose the minimum value across all rotations and reflections. Just like in Steerable NCA, we need to augment the target patterns with auxiliary channels in order to not create undesirable local minima.
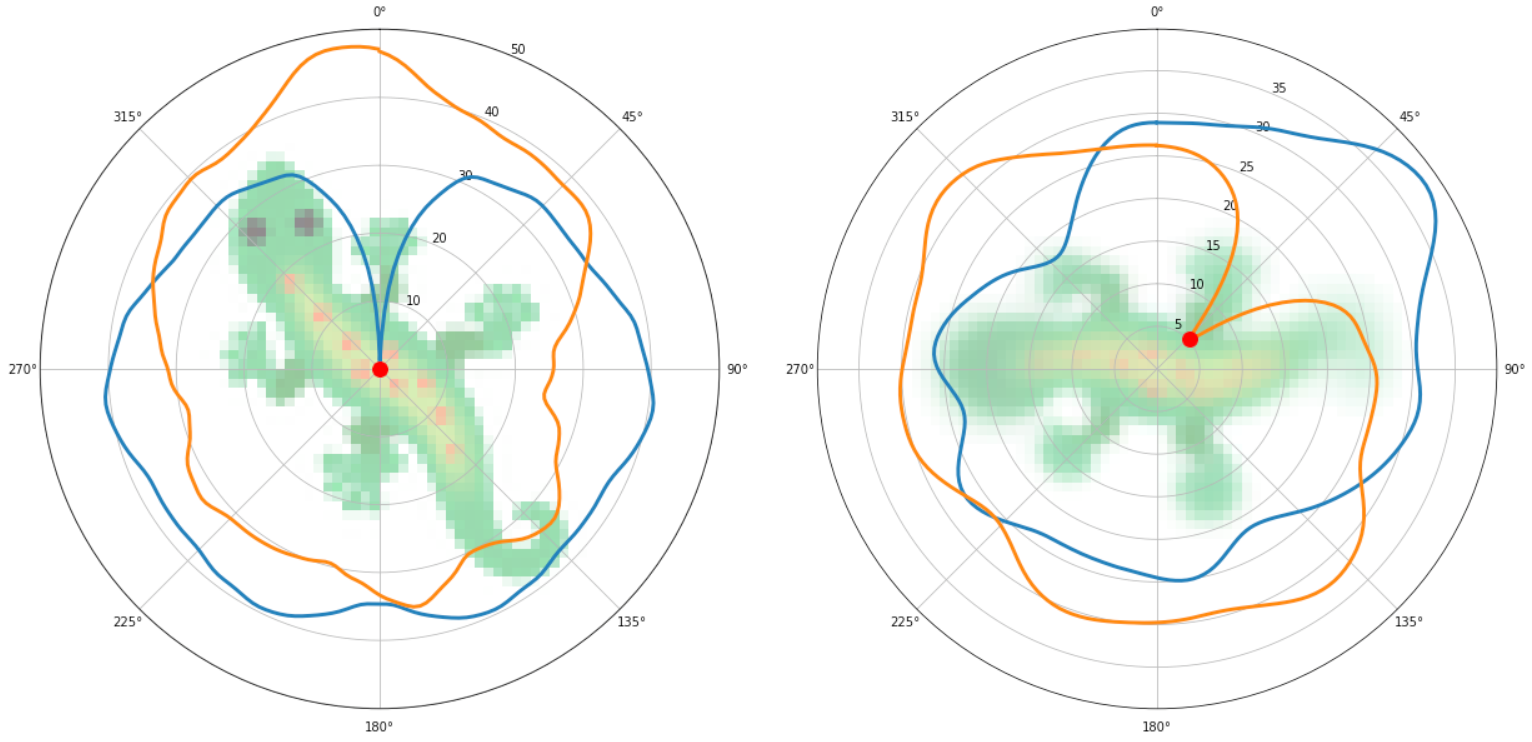
In the drawing above, on the left we show the loss of the target pattern with all of its rotations (blue ring) and all of its reflected rotations (orange ring). As you can see, there is only one point where the loss is truly minimised (a global minimum): when the reflection and rotation perfectly match the image (zero angle, no reflection). On the right, we show the loss computed by a developing pattern. In this case, the minimum loss is found at a 45 degree angle of the reflected target pattern.
Results
In general the behaviour of fully isotropic NCA where cells can only perceive the average state of their neighbours happens to be similar to the models with more sophisticated perception mechanisms. The simplicity of the perception allowed us to generalise rules trained on a square grid to other grid structures, including non-regular ones.
For example, the image below shows the result of running isotropic NCA of a set of Voronoi cells built on a set of poisson-disc sampled points. Cells perceive the average state of their neighbours weighted by the length of the shared edges. Interestingly, in this setting, some runs resulted in patterns where the tail was reflected with respect to the rest of the pattern.

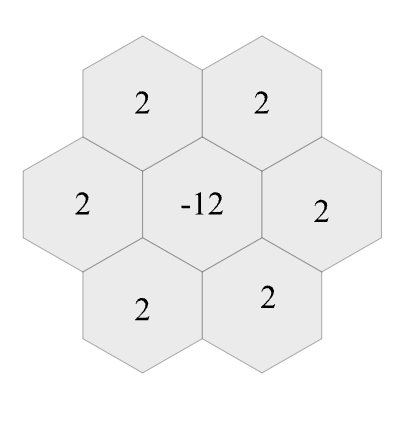
The supplementary demo also uses post-training adaptation to execute the square-grid trained NCA on a hexagonal grid. This is done by replacing the Lapplacian kernel with the hexagonal counterpart:
Structured seeds
With steerable NCA, an alternative to using the rotation-invariant loss was to break symmetries by means of carefully structured initial conditions. There, we used two different seeds to break the up-down symmetry of the system. We mentioned generalising this approach with structured seeds, and here we'll need a more comprehensive seed structure to break both the up-down symmetry and the left-right symmetry for isotropic NCA. Structured seeds are defined by their number of points, the initial channel encodings of those points, and their positions relative to one another. Using a structured seed composed of three distinct non-collinear points, we can effectively describe the model's rotation and reflection by defining two axial cues instead of one.

By breaking symmetries this way, we don't need to use any rotation- or reflection-invariant losses, and during training we continue to use the traditional pixel-wise L2 loss used to train anisotropic NCA, since the model can figure out from the seed how to coordinate to form a precise rotation and reflection. Also, like steerable NCA, this works without any need to augment the image with other auxiliary channels.
Distributing directional responsibility between the points enables us to manipulate the model's behaviour by performing entire plane isometries on the seed. In other words, we are no longer limited to translation and rotation; we can now affect reflection as well! For example, swapping two opposite seeds produces a reflection, and, if we rotate the seed by 72 degrees, we can expect the resultant pattern grown from this seed to be similarly rotated by 72 degrees.
Alternatively, a structured seed can be manually engineered to map key features of the target pattern to specific points of the seed. So long as there remain three or more non-collinear points, this configuration enables the model to break symmetries similarly to a more traditional three-point seed. These points are reconfigurable and, consequently, can be used to grow predictable out-of-training structural mutations of the target pattern. To change the configuration of a structured seed, all we need to do is modify the positions and channel encodings of its composite points, and voilà!
Maybe not so much… as we can see here, the stability of such irregular modifications is a little less reliable than that of simple plane isometries. However, manipulating the seed with a little more care often yields improved results; we find that seed replacement or removal tends to produce interesting - and, more importantly, predictable - patterns than seed scrambling.
Reaction-Diffusion models
The Differentiable Programming of Reaction-Diffusion Patterns (
Communication between neighbouring regions of space happens through the isotropic diffusion process that gradually blurs state fields. Thus, "reaction" must constantly work against diffusion to persist produced patterns.
In this work we focused on texture synthesis objective instead of pixel-wise pattern reconstruction, and made the emphasis on the continuous PDE interpretation of the pattern generation process. That's why we don't use "microscopic" stochasticity to break the symmetries, and simply initialise the fields to a random mixture of gaussian blobs.
PDE interpretation opens a number of possibilities that are not trivial to achieve with the discrete cell centric thinking. For example, we can vary the scale of produced textures by changing the ratio between the reaction and diffusion speeds. We can also apply the model to arbitrary manifolds with a defined diffusion operation.

Finally we can even apply the rule trained in a 2d space to a 3d volume, and often get surprisingly consistent structures!
Conclusion
In the broader context, the ideas of various transformation invariance and equivariance inspired a lot of successful developments in the field of Differentiable Programming. For example, Convolutional Neural Networks were motivated by the wish of giving the systems translational equivariance; pooling operations are a common way of achieving various invariances, for example to the position of a detected pattern. Graph Neural Networks and Attention mechanism in Transformers are largely motivated by permutation (in/equi)variance. Extensive discussion of such developments is provided by the Geometric Deep Learning project
To summarise, we described several methods of making NCA behaviour equivariant to rotations (Steerable NCA) and rotation-reflection (Isotropic NCA) transformations. We think that such NCAs may be better suited to model natural pattern formation and symmetry breaking processes. Techniques described here can also be useful for designing multiagent systems that require distributed coordination without external directional and positional cues, for example in swarm robotics applications.